Maîtriser le théorème de Pythagore de A à Z
Elèves de 4ème cette page vous est destinée! Vous venez de démarrer le nouveau chapitre de géométrie sur le théorème de Pythagore et vous êtes un peu perdus ? Pas de panique, on répond à toutes vos questions dans cet article! A la fin de cette page vous saurez quand et comment utiliser le théorème de Pythagore et comment bien rédiger pour obtenir tous les points le jour du contrôle. Avoir une bonne note est toujours notre objectif.
Allez c’est parti!
Quelle est la prorpiété de Pythagore ?
Ce théorème permet de calculer une longueur dans un triangle rectangle lorsque l’on connaît les deux autres. Mais que dit exactement la propriété ?
Énoncé du théorème de Pythagore:
Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égale à la somme des carrés des longueurs des deux autres côtés.
Qu’est que cela signifie ?
Avant toute chose, il faut savoir que l’hypoténuse est toujours le côté le plus grand dans un triangle rectangle (ou celui qui fait face à l’angle droit si vous préférez!).
Dans le triangle ci-contre, l’hypoténuse est donc le côté $AC$
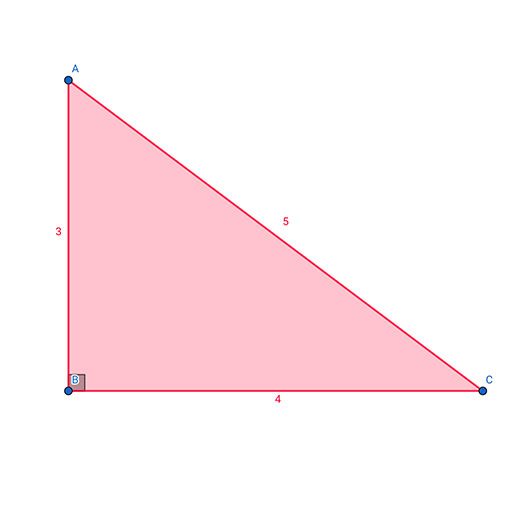
Dans le triangle ABC rectangle en B ci-contre, le théorème de Pythagore s’écrit donc ainsi:
$$AC^2=AB^2+BC^2$$
En effet, dans ce triangle, on sait que $AB=3$, $AC=5$ et $BC=4$
Si on calcule $AB^2+BC^2$ d’une part et d’autre part $AC^2$, ces deux quantités sont bien égales à 25
Astuce :
Pour écrire correctement la relation de Pythagore, il faut bien repérer quel côté est l’hypoténuse dans le triangle rectangle
Quand utilise-t-on le théorème de Pythagore?
Maintenant que nous savons comment écrire la propriété de Pythagore, nous allons voir à quoi elle sert et comment l’utiliser dans un exercice.
A quoi sert le théorème de Pythagore ?
Ce théorème permet de calculer une distance, la mesure d’un côté dans un triangle rectangle. Mais pour pouvoir l’utiliser, deux conditions doivent être remplies dans le cadre de l’exercice:
- Le plus important: le triangle doit être rectangle! Vous ne pouvez pas utiliser Pythagore si vous ne vous placez pas dans un triangle rectangle. Deux options s’offrent à vous; soit l’énoncé vous indique que le triangle est rectangle; soit vous avez démontré, au préalable que le triangle est rectangle.
- Enfin, vous devez impérativement connaître deux longueurs dans ce triangle rectangle
Vous pourrez alors calculer la longueur de l’hypoténuse ou la longueur d’un des côtés qui forment l’angle droit.
A retenir sur l’utilisation de Pythagore:
- Pythagore sert à calculer une longueur
- Je ne peux me servir de Pythagore que dans un triangle rectangle
- Je dois aussi connaître les longueurs de deux des côtés du triangle
Comment calculer l’hypoténuse avec le théorème de Pythagore?
Le mieux c’est de comprendre avec un exercice type.
Énoncé:
Soit DUC un triangle rectangle en C tel que $DC=5$ et $CU=12$. Calculer la longueur $DU$.
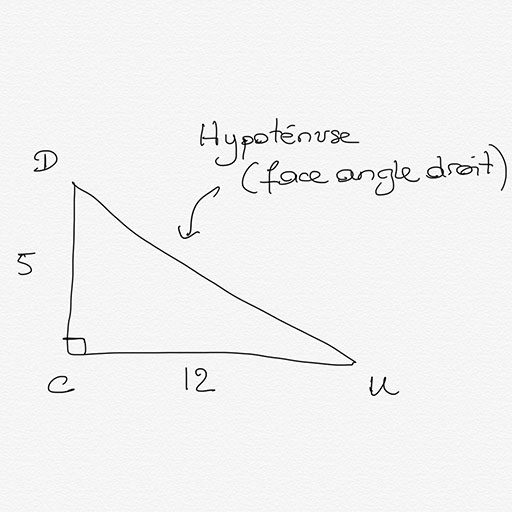
Démarche :
Je réalise un schéma à main levée où j’indique l’angle droit et les valeurs connues.
Cela me permet d’identifier quel côté est l’hypoténuse et que c’est elle que je dois calculer
Je peux alors écrire correctement le théorème de Pythagore:
$DU^2=DC^2+CU^2$
On remplace ensuite par les valeurs connues :
$DU^2=5^2+12^2$
Et je calcule:
$DU^2=25+144$
$DU^2=169$
J’applique ensuite la racine carrée pour faire disparaître le carré sur DU:
$DU=\sqrt{169}$
Et j’obtiens le résultat final :
$DU=13$
Vous avez maintenant utiliser la relation de Pythagore pour calculer l’hypoténuse d’un triangle rectangle. Voyons maintenant comment l’utiliser pour calculer un des côtés qui forment l’angle droit.
Comment calculer un des côtés de l’angle droit avec Pythagore?
Nous allons également traiter un exemple pour voir la différence.
Énoncé:
Dans le triangle TRI rectangle en R, on sait que $TR=6$ et $TI=10$. Calculer la longueur du côté $RI$
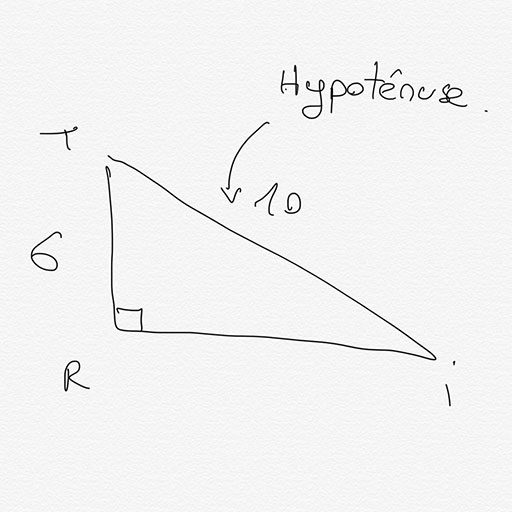
De la même façon que précédemment on réalise un schéma à main levée pour bien visualiser la situation.
On écrit alors la relation du théorème de Pythagore:
$TI^2=TR^2+RI^2$
Comme dans l’exemple précédent, on remplace par les valeurs :
$10^2=6^2+RI^2$
$100=36+RI^2$
Et on réalise une soustraction pour trouver la valeur de $RI^2$:
$RI^2=100-36=64$
Il n’y a plus qu’à appliquer la racine carrée pour déterminer la valeur de RI :
$RI=\sqrt{64}$
$RI=8$
A ce stade, vous savez vous servir et utiliser correctement la relation de Pythagore. Il ne manque plus qu’une seule chose pour faire de vous un maître de ce théorème: la rédaction.
Comment rédiger le théorème de Pythagore?
La rédaction est cruciale. Nous avons vu des élèves être sévèrement pénalisés pour ne pas avoir rédigé correctement leur démonstration. C’est tellement dommage d’avoir 10 quand on peut avoir 20! Alors voici, un exemple type, intégralement rédigé pour vous assurer tous les points le jour du contrôle.
Énoncé :
COU est triangle rectangle en O tel que $CO=27\:cm$ et $CU=45\:cm$. Calculer la longueur OU.
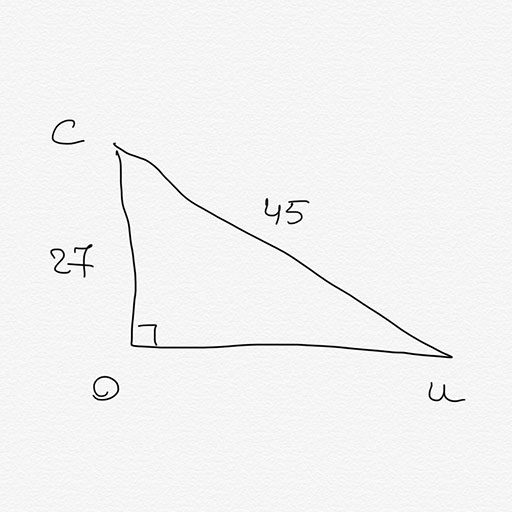
Rédaction type:
Dans le triangle COU rectangle en O, j’applique le théorème de Pythagore :
$CU^2=CO^2+OU^2$
$45^2=27^2+OU^2$
$2025=729+OU^2$
$OU^2=2025-729=1296$
$OU=\sqrt{1296}=36$
La distance OU mesure 36 cm
Point méthode: bien rédiger le théorème de Pythagore:
- Faire un schéma à main levée si la figure n’est pas demandée
- Ecrire que le triangle est rectangle et mentionner le théorème
- Ecrire la relation de Pythagore
- Remplacer par les valeurs et réalier les calculs
- Rédiger une phrase de conclusion en relation avec la question
Pour conclure sur Pythagore
Le théorème de Pythagore est une méthode parmi d’autres pour calculer une distance en géométrie. Le théorème de Thalès est également un outil de calcul de longueur, tout comme la trigonométrie dans le triangle rectangle. Cette dernière étant abordée en classe de 3ème.
Le théorème de Pythagore dispose d’une réciproque et aussi d’une contraposée. Nous les aborderons dans un prochain article.