Comment décomposer une fraction ?
Que signifie décomposer une fraction ?
Prenons par exemple la fraction $\frac{7}{2}$ à décomposer sous la forme d’un entier et d’une fraction inférieure à 1. Il faut bien comprendre ce que signifient le numérateur et le dénominateur de cette fraction.
Le dénominateur (ici, 2) représente le nombre total de parts égales que je dois couper dans mes pizzas. Dans ce cas précis, chaque pizza doit être coupée en 2 parts égales.
Le numérateur (ici 7) représente le nombre de parts que je souhaite prendre. Pour cette fraction, on souhaite pouvoir se servir 7 parts identiques.
On peut donc représenter la situation comme dans le schéma ci-contre.
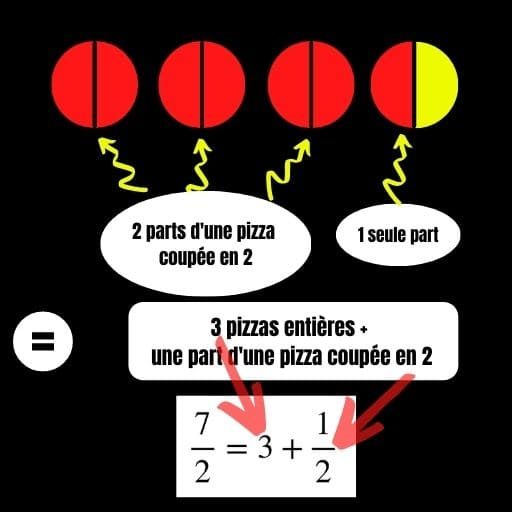
Pour pouvoir représenter la fraction $\frac{7}{2}$, il a donc fallu dessiner 3 pizzas complètes et prendre, en plus, 1 part d’une pizza coupée en 2. On peut donc décomposer la fraction $\frac{7}{2}$ en :
$$\frac{7}{2}=3+\frac{1}{2}$$
Il est évident que représenter des pizzas ou des gâteaux pour décomposer une fraction n’est pas le moyen le plus rapide et efficace de trouver la réponse! Néanmoins, ce graphique a l’avantage de permettre une bonne visualisation de la fraction.
Passons maintenant aux choses sérieuses…
Décomposer une fraction: étude d'un cas simple
Prenons maintenant le cas d’une fraction qu’il serait beaucoup trop compliqué de représenter graphiquement. Comme $\frac{32}{5}$.
On va tout simplement chercher, dans la table de 5, le plus grand multiple 5 plus petit que 28. Si tu connais tes tables de multiplications, cela ne pose aucune difficulté:
$5\times 6= 30$
$5\times 7=35$
On trouve ainsi le nombre entier de la décomposition de la fraction: ici 6, équivalent donc à 6 pizzas entières.
Il ne reste plus qu’à déterminer la fraction inférieure à 1. Pour cela, il suffit de trouver ici la différence entre 32 et 30. Soit 2. Il faudrait donc prendre encore 2 parts d’une pizza coupée en 5.
On obtient alors le résultat:
$$\frac{32}{5}=6+\frac{2}{5}$$
Synthèse de la première méthode
Afin de n’oublier aucune étape voici ce que tu dois faire pour arriver au résultat:
- chercher dans la table du dénominateur le multiple le plus grand possible inférieur au dénominateur
- Ensuite, calculer la différence entre le numérateur et le multiple que j’ai trouvé.
- Enfin, conclure avec la décomposition de la fraction
- connaître les tables de multiplications pour arriver rapidement au résultat
Cette méthode est extrêmement efficace tant que la valeur du numérateur est un nombre qui est dans la table du dénominateur. Si le numérateur est trop grand, il faut passer à la méthode suivante.
Décomposer une fraction avec une division euclidienne
Essayons maintenant de décomposer la fraction : $\frac{111}{4}$
Dans ce cas, le numérateur est bien trop grand. On ne connait la table de 4 que jusqu’à 40. On va donc tout simplement réaliser la division euclidienne de 111 par 4.
La division de 110 par 4 donne un quotient de 27 et un reste de 3:
$$110=4\times 24+3$$
Le résultat de cette division permet d’écrire la décomposition de la fraction. En effet, le quotient donne le nombre entier et le reste indique le nombre de parts de pizza supplémentaires à prendre. On obtient donc:
$$\frac{111}{4}=27+\frac{3}{4}$$
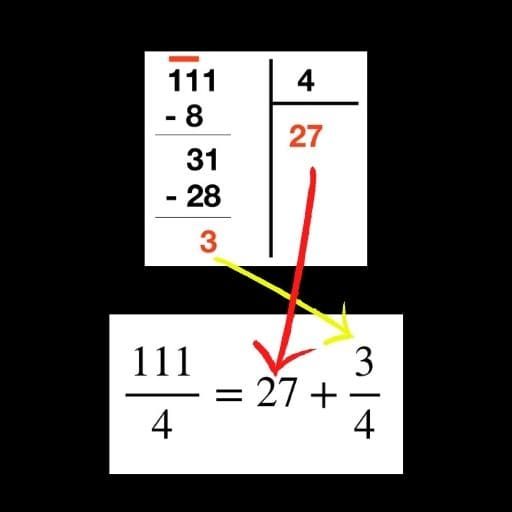
Pour réussir ma décomposition de fraction, je dois:
- faire la division euclidienne du numérateur par le dénominateur.
- noter la valeur du quotient qui représente le nombre entier de la décomposition
- noter également la valeur du reste qui intervient dans la fraction inférieure à 1 du résultat